工數-雲端
大碩研究所-理工研究所-化工所
- 授課師資程逸
- 課程類型大碩研究所
- 有效期限372天
- 上課方式 雲端課程
- 課程時數 152.2小時
- 上架日期
- 時數使用說明
課程名稱：工程數學─程逸
準備方法
熟悉上課內容
上課時專心聽課，盡量在課堂中就聽懂，不懂的地方利用下課時發問，在下一次上課前必須將前一次的內容熟讀，下一次上課前最好能做到不看講義與筆記都能回想起上一堂課大略內容的程度。
細讀講義
各章節前面一開始基礎的部分，如果基礎較差的同學，在課程一開始一定要多花點時間回去複習，練習課本習題。在較後面的章節，或是各章節中較為後面的內容，例如一階高次、高階非線性、Bessel方程式的解、Legendre方程式的解、求解特徵值特徵函數、偏微分方程式、矩陣應用題、向量三大定理、殘值定理之應用等，其實只要前面理論夠扎實，學習這些內容就是水到渠成。
勤做歷屆試題
當第一次唸完整個工數內容，開始第二次的複習時，建議同學一邊複習一邊整理出自己的定義定理筆記，這樣除了可以再次加深印象，而且在越接近考試時，這份筆記可以在最後的總複習時幫助同學快速複習重點。等到整個理論架構都熟悉了以後，再多做歷屆試題掌握近幾年重要題型，必可獲得好成績。
工程數學趨勢分析
由於研究所考試日期不斷的提前，壓縮了同學準備考試的時間，所以以往學長姊的考取經驗需要再稍微調整才可適用於現在的同學。
過去學長姊有很多是從三升四暑假開始努力聽課，秋季班到隔年三月努力複習、聽題庫班與做考古題，這個時間表由於研究所考試已經提前至2月初了，所以以學長姐的計畫來準備可能會太趕，建議現在準備研究所考試的同學要比以往學長姊再早一個學期(也就是三下)來準備會較為輕鬆。
各考試類別考情分析
| 微分方程式 | |
|---|---|
| 單元 | 必考系所 |
| CH1 一階ODE | 所有系所 |
| CH2 高階ODE | 所有系所 |
| CH3 級數解 | 所有系所 |
| CH4 Bessel方程式 | 所有系所 |
| CH5 Legendre方程式 | 所有系所 |
| CH6 邊界值問題 | 所有系所 |
| CH7 傅立葉 | 所有系所 |
| CH8 拉普拉斯 | 所有系所 |
| CH9 偏微分方程式 | 所有系所 |
上述所有系所包含力學類(機械、土木、航空、造船、工科)、電類(電子、電機、光電、電信的電波類組)、化工環工材料類
| 矩陣、向量、複變 | |
|---|---|
| 單元 | 必考系所 |
| CH10 矩陣 | 所有系所 |
| CH11 向量 | 力學類研究所、化環類研究所、部分電類研究所(主要為物理與光電類) |
| CH12 複變 | 力學類研究所 、化環類研究所、部分電類研究所(主要為物理與光電類) |
上述所有系所包含力學類(機械、土木、航空、造船、工科)、電類(電子、電機、光電、電信的電波類與通訊類)、化工環工材料類
工數章節重點
| 微分方程 | |
|---|---|
| 單元 | 重要性 |
| CH1 一階ODE | ★★★★ |
| 1.1 基本定義 | ★★★★ |
| 1.2 一階分離變數法 | ★★★★ |
| 1.3 一階正合ODE | ★★★★ |
| 1.4 一階線性ODE. | ★★★★ |
| 1.5 一階高次ODE | ★★★ |
| 1.6 應用題 | ★★ |
| 1.2 一階分離變數法 | ★★★★ |
| CH2 高階ODE | ★★★★ |
| 2.1 基本理論 | ★★★★ |
| 2.2 常係數線性常微分方程式 | ★★★★ |
| 2.3 等維方程式 | ★★★★ |
| 2.4 其他變係數常微分方程式 | ★★★★ |
| 2.5 高階非線性 | ★★★ |
| 2.6 應用題 | ★★★ |
| CH3 級數解 | ★★★★ |
| 3.1 基本定義與定理 | ★★★ |
| 3.2 常點展開求解ODE | ★★★★ |
| 3.3 規則奇點展開求解ODE | ★★★★ |
| CH4 Bessel方程式 | ★★★ |
| 4.1 Bessel方程式的解 | ★★★ |
| 4.2 可化為Bessel方程式 | ★★★ |
| 4.3 修正型Bessel方程式 | ★★ |
| CH5 Legendre方程式 | ★★★ |
| 5.1 Legendre方程式的解 | ★★★ |
| 5.2 Legendre多項式的補充 | ★★★ |
| CH6 邊界值問題 | ★★★★ |
| 6.1 函數的內積 | ★★★★ |
| 6.2 Sturm-Luouville問題 | ★★★★ |
| 6.3 特徵函數展開 | ★★★★ |
| CH7 傅立葉 | ★★★★ |
| 7.1 傅立葉級數 | ★★★★ |
| 7.2 半幅展開 | ★★★★ |
| 7.3 傅立葉積分 | ★★★★ |
| 7.4 傅立葉轉換 | ★★★★ |
| CH8 拉普拉斯 | ★★★★ |
| 8.1 拉氏轉換 | ★★★★ |
| 8.2 反拉氏轉換 | ★★★★ |
| 8.3 特殊函數之拉氏轉換 | ★★★ |
| 8.4 解微分方程與積分方程式 | ★★★★ |
| CH9 偏微分方程式 | ★★★★★ |
| 9.1 基本定義 | ★★★ |
| 9.2 波動方程式 | ★★★★★ |
| 9.3 熱傳方程式 | ★★★★★ |
| 9.4 拉氏方程式 | ★★★★★ |
| 9.5 非齊性PDE | ★★★★ |
| 9.6 轉換求解ODE | ★★★★ |
| 9.7 補充內容 | ★★★ |
| 複變、矩陣、向量 | |
|---|---|
| 單元 | 重要性 |
| 單元 | 重要性 |
| CH 10 矩陣 | ★★★★★ |
| 10.1 基本定義 | ★★★★ |
| 10.2 反矩陣 | ★★★★ |
| 10.3 列運算與行運算 | ★★★ |
| 10.4 線性系統與秩數(rank) | ★★★★★ |
| 10.5 行列式 | ★★★ |
| 10.6 特徵值與特徵向量 | ★★★★★ |
| 10.7 對角化與Jordan型 | ★★★★★ |
| 10.8 應用題 | ★★★★ |
| 10.9 補充內容 | ★★★ |
| CH11 向量 | ★★★★ |
| 11.1 基本定義 | ★★★ |
| 11.2 解析幾何 | ★★★ |
| 11.3 向量函數 | ★★ |
| 11.4 向量微分學 | ★★★★ |
| 11.5 向量積分學 | ★★★★ |
| CH12 複變 | ★★★★ |
| 12.1 基本定義 | ★★★ |
| 12.2 複變函數 | ★★★ |
| 12.3 複變微分學 | ★★★★ |
| 12.4 複變積分學 | ★★★★ |
| 12.5 常見複變積分應用 | ★★★★ |
| 12.6 特殊形式的積分 | ★★★★ |
| 12.7 映射 | ★★★ |
程逸老師教學特色
- 課程內容講解清楚，讓同學在最短時間內有效果的將工數學習好。
- 教學時以學生的角度思考，完全明白同學的盲點與問題所在。
- 課程內容隨著近幾年的歷屆試題而調整，讓學生在考試中更有優勢。
參考用書
- Erwin Kreyszig, Advanced Engineering Mathematics, 10th Edition.
- Peter V. O'Neil, Advanced Engineering Mathematics, 7th Edition.
- Dennis G. Zill & Michael R. Cullen, Differential Equations with Boundary - Value Problem, 4th Edition.
- 工數講義一~工數講義八, 程逸
程逸推薦試聽章節
- 基礎篇
- CH0、CH1、CH10，這些章節較前面小節即可
- 重點篇
- CH2較前面小節即可
研究所考試心得〡114年考取台大化工所榜首 蘇O閔
我不是應屆考生。 當年推甄失敗後，原本計劃在畢業後先尋找適合的工作， 但在瀏覽各大求職網站時發現，科技業若想找到較理想的職位，研究所學歷幾乎是必備條件。 因此在休息一段時間並仔細思考後，我決定報考研究所。 由於我自制力較弱，若沒有固定的時間安排容易怠惰， 因此我選擇了暑期的實體課程，跟著進度學習，平時則專注於刷題。 我並沒有固定的讀書時間，因為在沒有心情時強迫自己學習，效率反而不佳，甚至可能影響吸收效果。 但在狀態不理想時，我會適當調整心態，並盡快在一兩天內回到正軌，以維持學習進度。
19
2025/08/08
研究所考試心得〡114年考取台大化工所榜眼 邱O杰
我本身不太容易緊張，因此在準備期間，每天按計畫學習，剩餘時間適當放鬆，避免長時間處於緊張狀態。 適當的休息能幫助我維持良好狀態，迎接隔天的學習計畫。 此外，身邊的親友也會時常關心與支持我，讓我能夠保持正向態度，降低壓力，使備考過程相對輕鬆。
19
2025/08/08
研究所考試心得〡114年考取台大化工所 賴O諺
最大幫助的地方是提供我雲端課程，我不必去實體的地方上課， 我原本的學校中央大學地理位置偏僻，在桃園的山上，要去市區的話交通不便， 雖然這邊有平鎮學堂，但因為大三必修課的關係希望能自己安排念書進度與時間， 而雲端課程只要有網路的地方就可以啟動， 基本上不會遇到系統故障的問題。而且雲端系統有日曆以便事先安排進度， 這樣到時候在上課時對進度以及時間掌握比較有概念，不滿意再隨時調整即可。 另外，專業科目的林隆老師榜單一直都很亮眼，也是我考量的理由之一。
42
2025/08/08
研究所考試心得〡114年考取台大化工所 楊O翔
在中興大學前三年，是屬於比較混的， 在校成績排名位在中下，可以說是基礎觀念沒有很好。 在剛開始上林隆老師課時，幾乎等於從零開始， 很多基礎都是在大三下上課才慢慢打起來， 由此可知，能在這半年的期間翻盤考上頂大，TKB老師的教導功不可沒。
24
2025/08/08
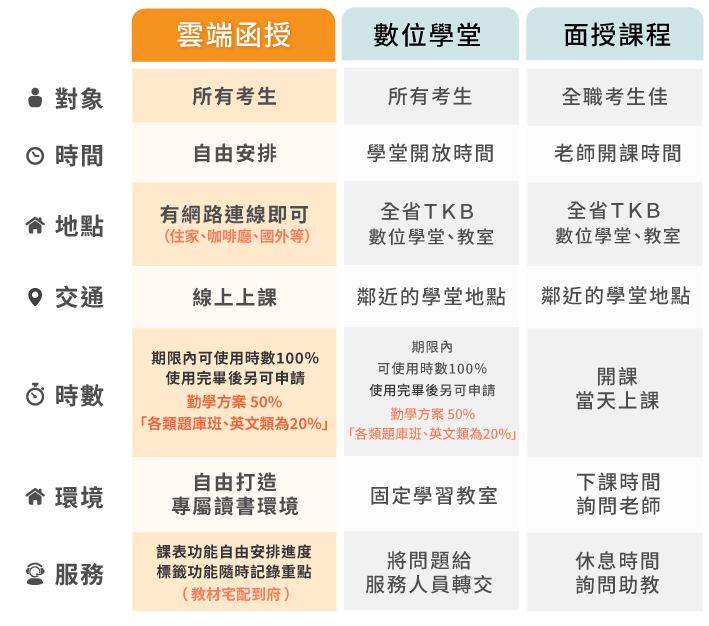
什麼是雲端函授?
為了提供同學或在職人士，擁有更多元自主的學習模式，讓學習貼近數位生活的時代。
只要登入 TKBTV 雲端學習平台，不限時間、地點，隨時都可上課學習。
不論是學生、家庭主婦、上班族等，皆可靈活運用時間，學習效果更加乘。
授課程內容
- 指定教材講義
- 課程需使用「電腦」「平板」「手機」觀看課程，不提供DVD光碟。
- 課程有時數限制，時數僅在撥放狀態才會進行扣除。 時數使用說明
如何查看課程
首次使用，請至 TKBTV 下載並安裝「課程播放器」。
播放檔案大小為 531 MB，為提供學員觀看課程之品質、防護安全，皆經過多重防毒保護、下載無疑。
設備需求
- 電腦硬體需求
- 最低配備：CPU Pentium 4以上
- 記憶體：1GB RAM
- 網路設備：有線網路、無線WiFi、行動網路
- 其他週邊需求：耳機或喇叭
- 執行環境
- 電腦: Windows10、Mac10.13、Linux
- APP：Android 4.4 以上、IOS 9 -14.4以上
- TV雲端播放器最新版本4.9連線需求
- 實測網路頻寬約 30M以上
台大網路測速、Speedtest網路測速 - 以行動裝置觀看雲端教育課程，宜採用WiFi觀看為優先選擇。(但若使用WiFi觀看仍有不順或斷線情形，則建議改採網速較穩定的有線網路進行課程觀看)
付款方式
- 信用卡
一次付清
單筆滿三萬可分三期零利率（合作銀行：玉山、台新、國泰） - 轉帳
手機網路銀行
ATM繳費功能
銀行臨櫃
課程聲明
本公司於網站上販售的雲端函授商品與相關課程教材屬於授權著作財產商品，請勿重製影音商品與教材，違者需承擔相關法律責任。
本公司保有異動課程、價格之權利，若有任何疑慮歡迎與我們 或 聯繫。
提供諮詢服務包含：
- 對於商品不理解的地方都可以一對一詢問。
- 線上訂購特殊需求：更換師資、更換課程等。
- 最新考情資訊與優惠活動分享。
- 課程有時數限制，時數僅在撥放狀態才會進行扣除。 時數使用說明
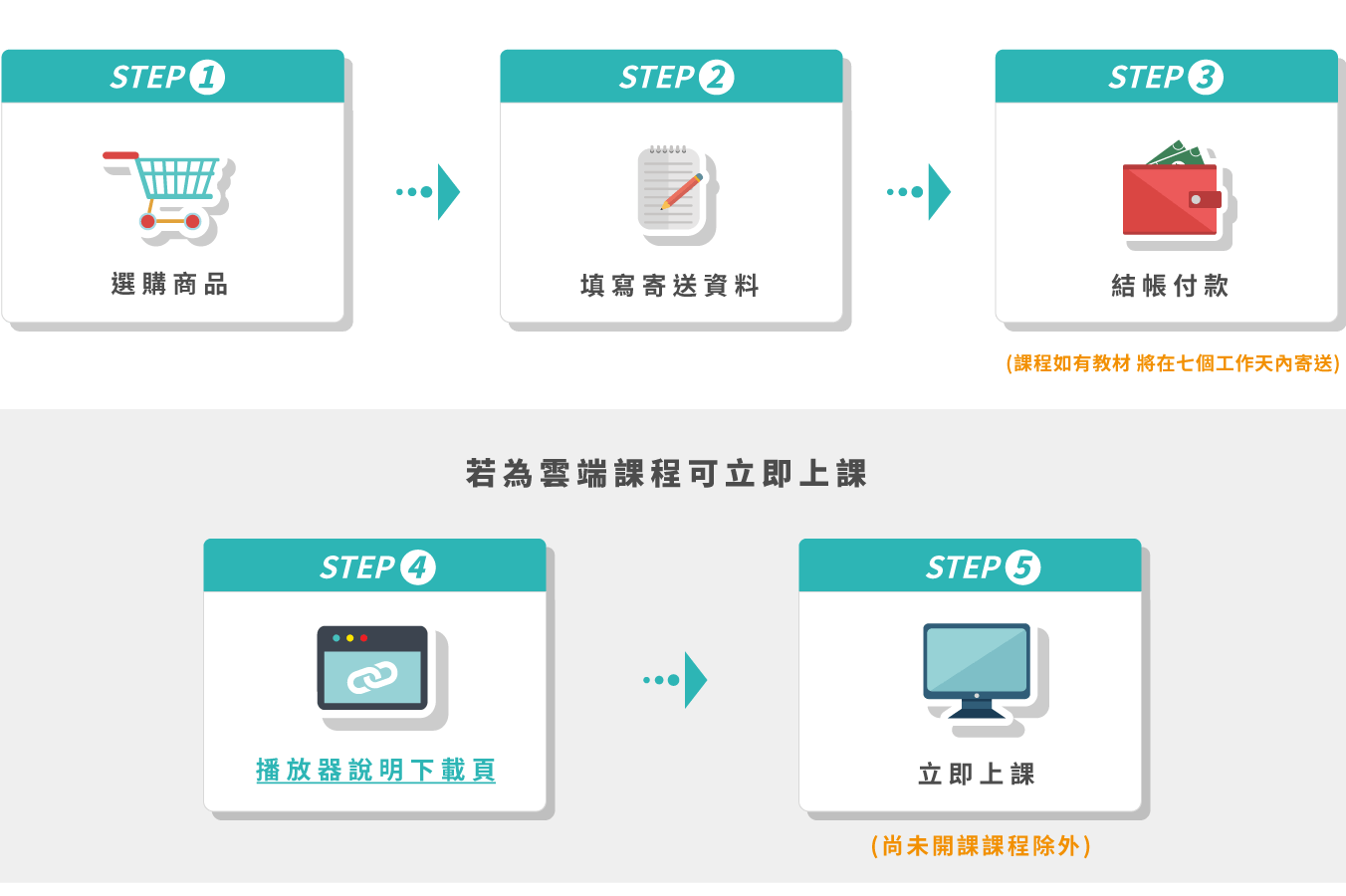
課程購買方式
- 確認購買商品
- 加入購物車
- 填寫訂購資料
- 送出訂單
- 進行付款
- 完成訂購
程逸
- TKB專任教師
學 歷
- 國立台灣大學博士候選人
- 國立台灣大學碩士
經 歷
- TKB微積分專任老師
- TKB工程數學專任老師
- TKB機率專任老師
- 百官網工程數學專任老師
授 課 科 目
- 工程數學
- 機率
- 微積分
- 線性代數
著 作
- 2014試題大補帖工程數學
- 高普特考2015試題大補帖工程數學
- 高普特考2016試題大補帖工程數學
- 鐵路特考2016試題大補帖電力工程類(合著)
- 研究所105工程數學考題精解(合著)
- 研究所2017試題大補帖工程數學(合著)
- 高普特考2017試題大補帖工程數學
- 鐵路特考2017試題大補帖電力工程類(合著)
- 研究所2018試題大補貼工程數學(合著)
- 技師考試2018試題大補貼電機工程技師(合著)
- 鐵路特考2018試題大補貼電力工程類(合著)
- 研究所2019試題大補帖通訊所(合著)
- 公職考試2019試題大補帖工程數學
- 研究所2020試題大補帖通訊所(合著)
