演算法
大碩研究所-理工研究所-資工所
演算法準備方法
(以下科目介紹由林立宇老師提供)
學生須對於課堂上所提及的所有觀念,有充分的理解。
不斷地反覆思考,以熟悉各種演算法設計的策略與分析方式。
演算法一科十分注重學生的獨立思考能力。
在理解了上課內容之後,學生將對於各類演算法的分析與策略,有基本的理解。
然而,光是上課聽講將不足以達到學以致用的境界。
如果想利用所學的觀念,來創造出新的演算法並用以解決問題,則必須透過大量的解題訓練。
在做題目的過程中,培養自身的思考能力,如此一來才能真正通透所學內容,徹底掌握演算法的精妙之處。
學生可透過練習課程講義中,列於各個章節末的習題,以達成解題思維訓練的目標。
演算法趨勢分析
在研究所考試中,演算法為全臺所有知名資工系所的重點考試科目之一。
例如以下大學:
- 臺灣大學(資料結構與演算法)
- 交通大學(資料結構與演算法)
- 清華大學(基礎計算機科學)
- 中央大學(資料結構與演算法)
- 成功大學(程式設計)
其中,著名的演算法策略像是 Divide-and-conquer(CH2)與 dynamic programming (CH3)。
與一些經典的圖形演算法(CH4)皆為各校的考試重點範圍。
另外,演算法時間複雜度分析,亦為所有資工系學生必備的基礎知識(CH1)。
近幾年,各校也越來越重視,學生對於計算理論基礎知識的觀念理解(CH6)。
計算幾何(CH5)的部分,因為相對於其他主題而言,較為獨立並具有其獨特性。
且其涵蓋範圍極廣,使得一般學校在課程安排上,難以有充分的時間介紹其內容。
因此出現在考題中的比例偏低。
除此之外,本課程所提及的章節,皆為各個名校的考試重點。
演算法章節重點
| 章節名稱 | 重要度 |
|---|---|
| Asymptotic notation | ★★★ |
| Recurrence relation | ★★★ |
| Amortized analysis | ★ |
| 章節名稱 | 重要度 |
|---|---|
| Introduction | ★★★ |
| The maximum subarray problem | ★★★ |
| Matrix multiplication | ★★★ |
| The selection problem | ★★★ |
| The closest pair problem | ★ |
| 章節名稱 | 重要度 |
|---|---|
| Introduction | ★★★★ |
| The rod cutting problem | ★★★★ |
| The knapsack problem | ★★★★★ |
| Matrix-chain multiplication | ★★★★★ |
| Optimal binary search tree | ★★★★★ |
| Longest common subsequences | ★★★★★ |
| The KMP algorithm | ★★ |
| 章節名稱 | 重要度 |
|---|---|
| Breadth-first search | ★★★ |
| Depth-first search | ★★★★ |
| Single-source shortest paths | ★★★★★ |
| All-pairs shortest paths | ★★★★★ |
| Minimum spanning trees | ★★★★ |
| Maximum flow | ★★★★★ |
| 章節名稱 | 重要度 |
|---|---|
| Line segment intersection | ★ |
| Convex hull | ★★ |
| 章節名稱 | 重要度 |
|---|---|
| Complexity class | ★★★★★ |
| NP-complete problems | ★★★★ |
| Approximation algorithms | ★★ |
林立宇老師教學特色
-
以簡潔易懂的例子說明各種演算設計方法的關鍵思維。
-
掌握困難演算法的重點精神,以清晰且簡單的敘述使學生能夠理解各個著名演算法策略背後的核心思想。
-
講學細心,能夠清楚了解學生在學習時容易產生困惑之處,並在課堂上加以提點。
演算法參考用書
- 林立宇編,歷年演算法上課講義
- Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein, Introduction to Algorithms.
程逸推薦試聽章節
基礎篇:
- 第 3.1 章
- 第 3.2 章
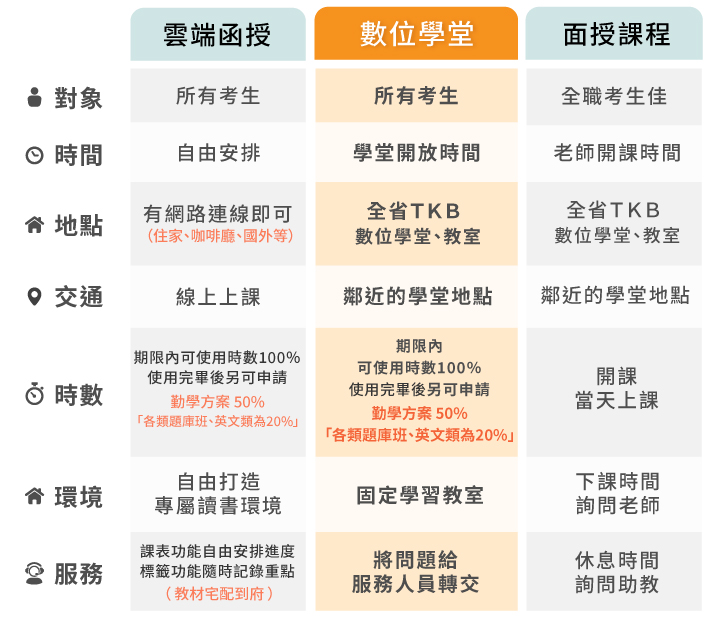
什麼是數位學堂?
數位學堂與一般線上課程不同,同學需要「到教室觀看影片課程」。
由學員自主安排上課時間和學習進度的方式,讓學員沒有缺課、補課的煩惱,並採「集中學習」培養學員高度的自律性。
同時提供了一個寬敞舒適且配備頂級硬體設備的實體環境,透過高速穩定的網路傳輸,讓學生能獲得最高品質的學習效果。
對大多數的在職進修者而言,是最具彈性的學習選擇。

授課程內容
數位學堂採用上網「預約座位」機制,同學可到網站上依預約的學習時段,到相關教室上課。
每次預約的時間分成「 200 分鐘」與「100 分鐘」兩類場次,全台數位學堂的場次,會根據據點不同進行調整。
一天約有 2 至 4 場次可供選擇。
此外,數位學堂的學習時數計算方式,是以每次的「上課時間」而非「課堂數量」計算。
因此,若無法準時至數位學堂上課,請在上課前一天到網站上取消預約,讓系統回填你的學習時數,避免讓自己的學習權益損失。

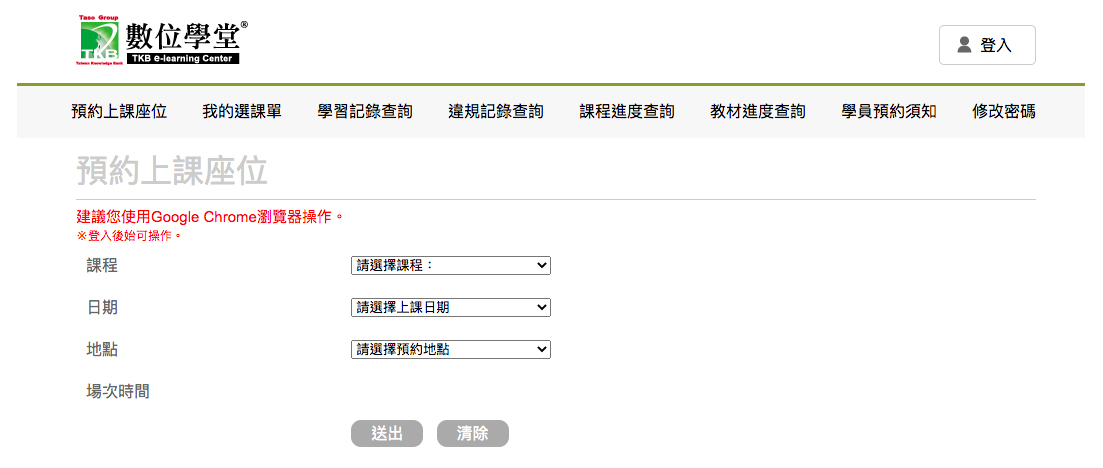
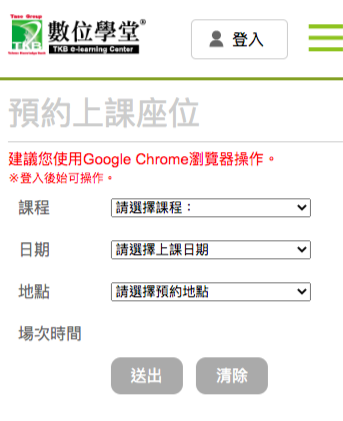
如何預約課程
- 至數位學堂的首頁,點選「學員專區」。
- 進入「學員專區」後,點選「學員預約上課座位」,出現登錄畫面,輸入您的帳號及密碼。
- 登入後,在左方點選「預約座位」的選項後,會出現預約上課座位的欄位。
- 按欄位選擇你預計上課的課程名稱、上課日期、上課地點以及上課的時段,一切填妥後,點選「送出」的選項。
- 你所預約的時段便會記錄在數位學堂的資料庫中,並出現你所預約的上課時段及座位。
服務據點
目前全台已經有 28 個數位學習中心,並預計將持續增設數位學習中心,提供學員更完善、更便利的學習服務。
| 地點 | 聯絡地址 | 電話 |
|---|---|---|
| 台北 | 台北市開封街一段32號3、4樓 | TEL:(02)2331-5377 |
| 景美 | 台北市文山區羅斯福路6段234-1號5樓 | TEL:(02)5571-3131 |
| 新莊 | 新北市新莊區建興街9號1樓 | TEL:(02)5578-6558 |
| 淡江 | 新北市淡水區大忠街161號1樓 | TEL:(02)2625-7982 |
| 三峽 | 新北市三峽區國學街40號2樓 | TEL:(02)5578-8140 |
| 基隆 | 基隆市中正區義一路4號2樓 | TEL:(02)5596-9013 |
| 宜蘭 | 宜蘭市中山路二段145號二樓之1 | TEL:(03)931-4228 |
| 東華 | 花蓮縣壽豐鄉志學村中正路138-3 | TEL:(03)800-3120 |
| 花蓮 | 花蓮縣花蓮市中山路719號 | TEL:(03)856-8255 |
| 林口 | 桃園縣龜山鄉復興ㄧ路128-2號3樓 | TEL:(03)318-5288 |
| 桃園 | 桃園市民權路6號7樓之一 | TEL:(03)337-1118 |
| 中壢 | 中壢市新興路102巷9號6樓 | TEL:(03)468-1028 |
| 中央 | 中壢市五權里2鄰五興路329號 | TEL:(03)420-6169 |
| 新竹 | 新竹市民族路31號9樓 | TEL:(03)523-8442 |
| 苗栗 | 苗栗市為公路8號3樓 | TEL:(037)273-223 |
| 台中 | 台中市綠川西街73號1~2樓 | TEL:(04)2229-0445 |
| 逢甲 | 台中市西屯區河南路2段319號3樓 | TEL:(04)2452-3305 |
| 東海 | 台中市龍井區臺灣大道五段43-1號1樓 | TEL:(04)2632-6812 |
| 彰化 | 彰化縣彰化市中正路二段79號 | TEL:(04)723-9550 |
| 斗六 | 雲林縣斗六市鎮北路34號 | TEL:(05)535-0071 |
| 虎尾 | 雲林縣虎尾鎮林森路2段268號 | TEL:(05)632-5477 |
| 嘉義 | 嘉義市北榮街219號 | TEL:(05)229-0125 |
| 民雄 | 嘉義縣民雄鄉大學路一段439號 | TEL:(05)300-8168 |
| 台南 | 台南市中西區成功路75號1樓 | TEL:(06)225-3462 |
| 楠梓 | 高雄市楠梓區建楠路236號5樓 | TEL:(07)355-8783 |
| 高大 | 高雄市楠梓區援中路310號 | TEL:(07)958-1636 |
| 高雄 | 高雄市新興區八德一路332號3樓 | TEL:(07)235-5618 |
| 屏東 | 屏東縣屏東市南昌街1號 | TEL:(08)765-2590 |
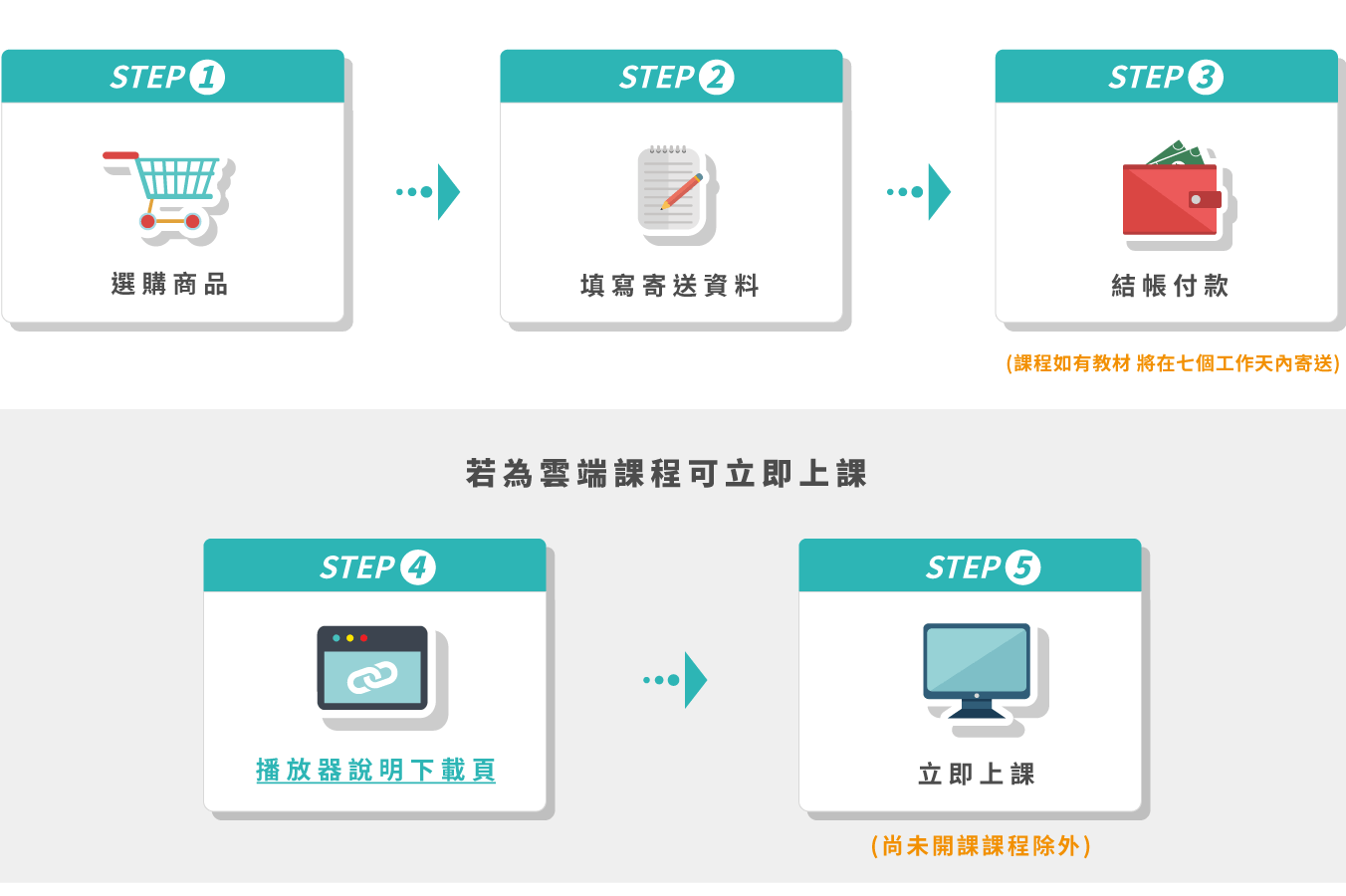
課程購買方式
- 確認購買商品
- 加入購物車
- 填寫訂購資料
- 送出訂單
- 進行付款
- 完成訂購


林立宇
- 國立台灣大學 資訊工程 博士
- 演算法研發工程師
- 大碩補習班講師
- 將繁雜觀念濃縮精華,高效率準備考試
- 將重點觀念拆解透徹,立刻就變得輕鬆易懂
- 用心編排課程講義,熟讀考試考點
- 提供大量練習題目,幫助同學增加熟練度
- 演算法
- 離散數學
- 線性代數